既然涉及的是旅游搜索,那就不能少了空间搜索的内容。现在移动设备之广泛想必不必多说。根据eMarketer的新数据,2015年全球智能手机用户将达到19.1亿,2016年该指数将增长12.6%达到21.6亿。智能手机都会带有GPS模块,现在一个APP不获取下用户位置都觉得是吃亏,不过这也用户隐私的侵犯也很严重,尤其是在Android生态圈中,不过现在各大手机厂商的系统都对这一块做了一些限制。
空间搜索,又名Spatial Search,基于空间搜索技术,可以做到:
- 对Point(经纬度)和其他的几何图形建索引
- 距离计算:根据给定点计算它到其他点的距离。
- 限定框过滤器:查找某些特定区域内所有匹配项(文档)。
- 排序:根据到固定点的距离对搜索结果进行排序。
- 相关度改进:使用距离作为记录中的增强因素,同时允许其他因素发挥作用。
- 查询解析:在给出位置的地址或其他一些用户规定时,创建可用于根据索引数据进行搜索的编码表示。
空间搜索原理
在Solr中,空间搜索主要基于GeoHash和Cartesian Tiers 2个概念来实现。下面先来讲解一下这两个算法,虽然这两种算法可以很容易在网上找到资料,但是我在这里对其进行总结,并根据之前自己的知识和相似的技术、算法思想进行对比。后面将会是和Solr相关的如何进行配置和查询,虽然这些算法的实现比较复杂,好在Solr已经帮我们做好了,通过配置就可以使用。当然这里最需要感谢的美团的技术团队,这么无私的把这些技术分享出来,我基本上是靠美团的这篇文章来完成了这个模块的工作。
GeoHash算法
GeoHash即Geology和Hash的组合,使用hash算法的方法对地理信息进行编码,要想充分了解GeoHash,我们先来了解Hash。
各种Hash及其核心思想
Hash(散列)算法,是一种从任何一种数据中创建小的数字“指纹”的方法。散列函数把消息或数据压缩成摘要,使得数据量变小,将数据的格式固定下来。该函数将数据打乱混合,重新创建一个叫做散列值(hash values,hash codes,hash sums,或hashes)的指纹。
计算机中有关Hash的应用有很多的,例如java的HashMap、Hash Table、数据加密、数据完整性、错误校正等方面都有应用。它的基本思想上面的Wikipedia已经定义的比较好了,我来分享下我的见解,hash就是把数据按照某种规则进行重组再表示,这个再表示比原始的数据量要小,其实是有损的转换,因此不能从再表示中还原数据。另外由于再表示的取值空间比较小,会有不同的原始数据经过Hash之后得到相同的再表示,这也就意味着冲突,好的转换规则能最低限度的降低冲突概率。
和GeoHash比较相近的应用是Hash Table,它通过关键码值(Key value)来访问数据,把key通过一个hash函数生成Hashcode,这个Hashcode对应一个位置,而其value就放在这个位置,相当于是key和value所在位置的一个映射。我们知道线性的数据结构能够通过index(下标)来快速获取数据(非线性需要遍历才能找到),我们可以直接把下标当做key,这样的<key,value>也可以快速找到,但希望的是key可以是任何字符,那么经过hash函数的转换,Hash Table应运而生。
Hash Table是为了解决查询速度的问题,GeoHash当然也是为了解决这个问题,它主要解决的是地理位置的查找,不过其复杂程度比Hash Table高一些,不过也算比较容易理解。
GeoHash初识
其实GeoHash就是将二维的经纬度转换成字符串,并且这些字符串有个特征是同一个地区的前缀N位是相同的,如果两点的GeoHash字符串前缀相同的位数越多表示这两点越接近,因此将距离的计算转换成字符串相同位数的比较,虽然是其基本原理如此常见,但运算量的减小确是非常巨大的。
为了能让大家对我上面说的概念有个更直观的了解,于是我很恬不知耻地借用别人的图片来给大家看,也是蛮拼(lan)的。
上图可以看到每一个字符串代表了一个矩形区域(为啥是矩形不是方形?下面再说),只要是这个区域内的所有点经过GeoHash算法之后前5位一定是相同的。这就有个好处,那就是缓存啊,把数据按照区域缓存起来加快访问速度和减小负载,真是机智。
上面的图是啥意思呢?字符串越长,表示的范围越精确。5位的编码能表示10平方千米范围的矩形区域,而6位编码能表示更精细的区域(约0.34平方千米),也就是说在大格子里面画小个子,也从正面说明了前缀相同的位数越多表示这两点越接近。
GeoHash算法步骤
我们都知道地球的纬度为-90~90,经度为-180~180,我就用美团这篇文章的数据来讲吧。例如纬度为39.92324,经度为116.3906(这货真懒)
二分编码
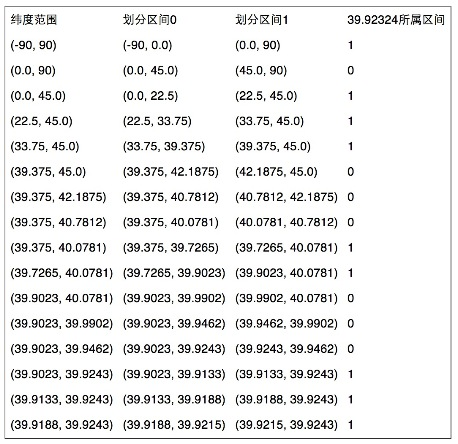
1) 对区间[-90,90]进行二分为[-90,0),[0,90],称为左右区间,可以确定39.92324属于右区间[0,90],给标记为1;
2) 接着将区间[0,90]进行二分为 [0,45),[45,90],可以确定39.92324属于左区间 [0,45),给标记为0;
3) 递归上述过程,39.92324总是属于某个区间[a,b],随着每次迭代区间[a,b]总在缩小,并越来越逼近39.928167;
4) 如果给定的纬度(39.92324)属于左区间,则记录0,如果属于右区间则记录1,这样随着算法的进行会产生一个序列1011 1000 1100 0111 1001,序列的长度跟给定的区间划分次数有关。
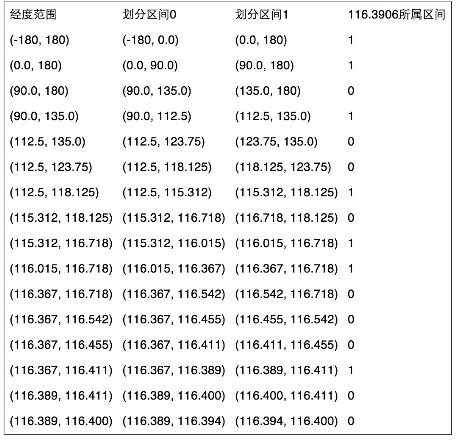
 5) 同理,地球经度区间是[-180,180],对经度116.3906进行编码的过程也类似的二分编码,过程如下:
5) 同理,地球经度区间是[-180,180],对经度116.3906进行编码的过程也类似的二分编码,过程如下:
组码&Base32编码
通过上述计算(图中只显示16次二分,共20次),纬度产生的编码为1011 1000 1100 0111 1001,经度产生的编码为1101 0010 1100 0100 0100。偶数位放经度,奇数位放纬度。因为经纬度都分别二分了20次,现在要组合成一个二十位数,这个数从左往右(纬度表示为lat,经度表示为lng)
| 40 | 39 | 38 | 37 | 36 | ... |
|---|---|---|---|---|---|
| lng[20] | lat[20] | lng[19] | lat[19] | lng[18] | ... |
| 1 | 1 | 1 | 0 | 0 | ... |
把2串编码组合生成新串:11100 11101 00100 01111 00000 01101 01011 00001。
这里解释下为什么前面说这些字符串分的是矩形格子,说到这里,相信大家都明白了,经度的取值范围是纬度的一倍,但都是只二分了10次,相同位数的表示,经度所能表示的长度也是纬度的一倍,在地图上就是宽宽的格子。
最后使用用0-9、b-z(去掉a, i, l, o)这32个字母进行base32编码,首先将11100 11101 00100 01111 00000 01101 01011 00001转成十进制 28,29,4,15,0,13,11,1,十进制对应的编码就是wx4g0ec1。同理,将编码转换成经纬度的解码算法与之相反,具体不再赘述。
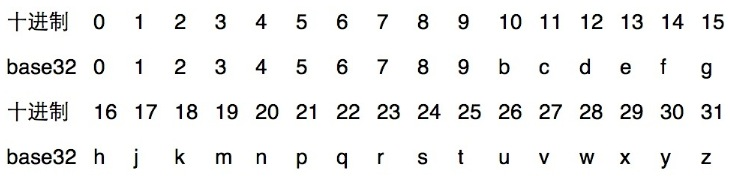
GeoHash Base32编码长度与精度
下表摘自维基百科:http://en.wikipedia.org/wiki/Geohash
可以看出,当geohash base32编码长度为8时,精度在19米左右,而当编码长度为9时,精度在2米左右,编码长度需要根据数据情况进行选择。
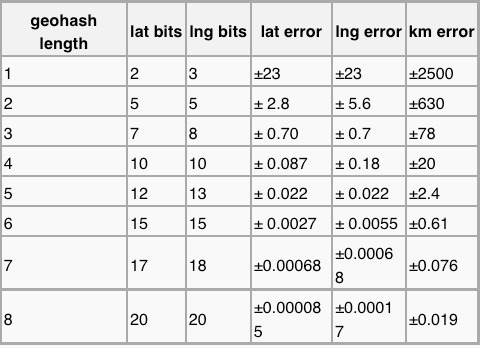
GeoHash算法依据的数学原理
算法有了,但是为什么是这样的呢,大牛们是怎么想出这个算法的呢?一切还要从数学说起,可怜我数学水平一般,下面的这些东西一知半解,直接搬过来了。
如图所示,我们将二进制编码的结果填写到空间中,当将空间划分为四块时候,编码的顺序分别是左下角00,左上角01,右下脚10,右上角11,也就是类似于Z的曲线,当我们递归的将各个块分解成更小的子块时,编码的顺序是自相似的(分形),每一个子快也形成Z曲线,这种类型的曲线被称为Peano空间填充曲线。
这种类型的空间填充曲线的优点是将二维空间转换成一维曲线(事实上是分形维),对大部分而言,编码相似的距离也相近, 但Peano空间填充曲线最大的缺点就是突变性,有些编码相邻但距离却相差很远,比如0111与1000,编码是相邻的,但距离相差很大。
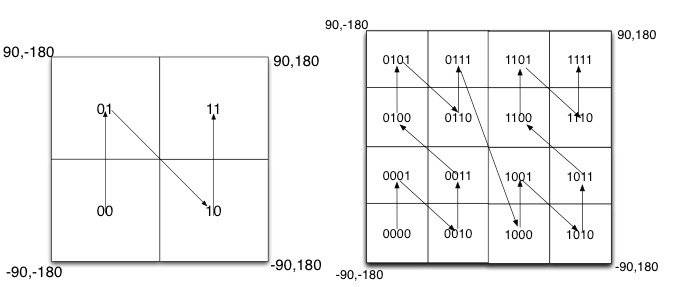
除Peano空间填充曲线外,还有很多空间填充曲线,如图所示,其中效果公认较好是Hilbert空间填充曲线,相较于Peano曲线而言,Hilbert曲线没有较大的突变。为什么GeoHash不选择Hilbert空间填充曲线呢?可能是Peano曲线思路以及计算上比较简单吧,事实上,Peano曲线就是一种四叉树线性编码方式。

应注意的问题
1) 由于GeoHash是将区域划分为一个个规则矩形,并对每个矩形进行编码,这样在查询附近POI信息时会导致以下问题,比如红色的点是我们的位置,绿色的两个点分别是附近的两个餐馆,但是在查询的时候会发现距离较远餐馆的GeoHash编码与我们一样(因为在同一个GeoHash区域块上),而较近餐馆的GeoHash编码与我们不一致。这个问题往往产生在边界处。
2)
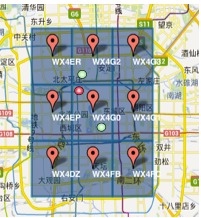
解决的思路很简单,我们查询时,除了使用定位点的GeoHash编码进行匹配外,还使用周围8个区域的GeoHash编码,这样可以避免这个问题。
2) 我们已经知道现有的GeoHash算法使用的是Peano空间填充曲线,这种曲线会产生突变,造成了编码虽然相似但距离可能相差很大的问题,因此在查询附近餐馆时候,首先筛选GeoHash编码相似的POI点,然后进行实际距离计算。
Cartesian Tiers算法
Cartesian Tiers 是笛卡尔层的意思,笛卡尔我们应该很熟悉,是一个伟大的哲学家和数学家,这里讲到笛卡尔是和笛卡尔坐标系有关。笛卡尔分层模型的思想是将经纬度转换成更大粒度的分层网格,该模型创建了很多的地理层,每一层在前一层的基础上细化切分粒度,每一个网格被分配一个ID,代表一个地理位置。
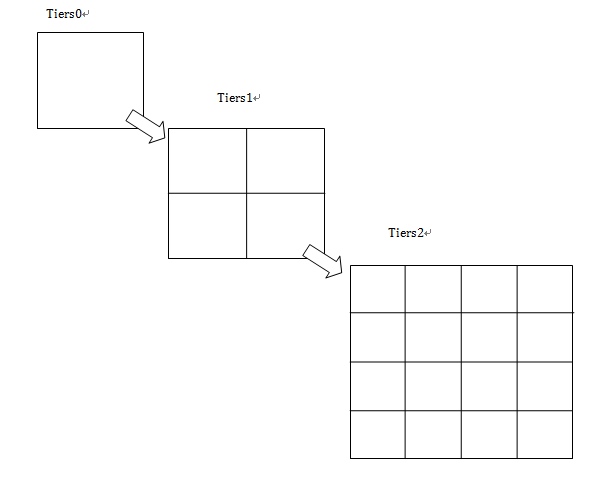
每层以2的平方递增,所以第一层为4个网格,第二层为16 个,所以整个地图的经纬度将在每层的网格中体现:
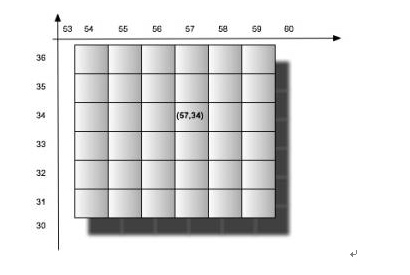
那么如何构建这样的索引结构呢,其实很简单,只需要对应笛卡尔层的层数来构建域即可,一个域或坐标对应多个tiers层次。也即是tiers0->field_0,tiers1->field_1,tiers2-field_2,……,tiers19->field_19。(一般20层即可)。每个对应笛卡尔层次的域将根据当前这条记录的经纬度通过笛卡尔算法计算出归属于当前层的网格,然后将gridId(网格唯一标示)以term的方式存入索引。这样每条记录关于笛卡尔0-19的域将都会有一个gridId对应起来。但是查询的时候一般是需要查周边的地址,那么可能周边的范围超过一个网格的范围,那么实际操作过程是根据经纬度和一个距离确定出需要涉及查询的从19-0(从高往低查)若干层对应的若干网格的数据。那么一个经纬度周边地址的查询只需要如下图圆圈内的数据:
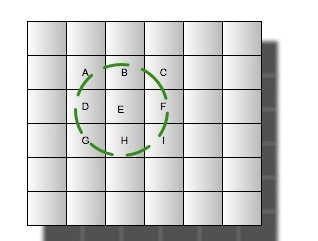
由上可知,基于Cartesian Tier的搜索步骤为: 1、根据Cartesian Tier层获得坐标点的地理位置gridId 2、与系统索引gridId匹配计算 3、计算结果集与目标坐标点的距离返回特定范围内的结果集合 使用笛卡尔层,能有效缩减少过滤范围,快速定位坐标点。
笛卡尔层在Lucene中对空间地理位置查询最大的用处在查找周边地址的时候有效的减少查询量,即将查询量可以控制在分层后最小的网格中的若干docId。
这个思想的另外一个应用在地图的展现上,整个世界地图相当于是第一层,只有各个国家名字;我们对某个块进行放大,例如中国这一块,会加载省份,这相当于进入第二层;对某个省份进行放大会继续加载城市,这相当于第三层。当然实际的分层应该比较多的,分层越多缩放的时候当然越流畅。
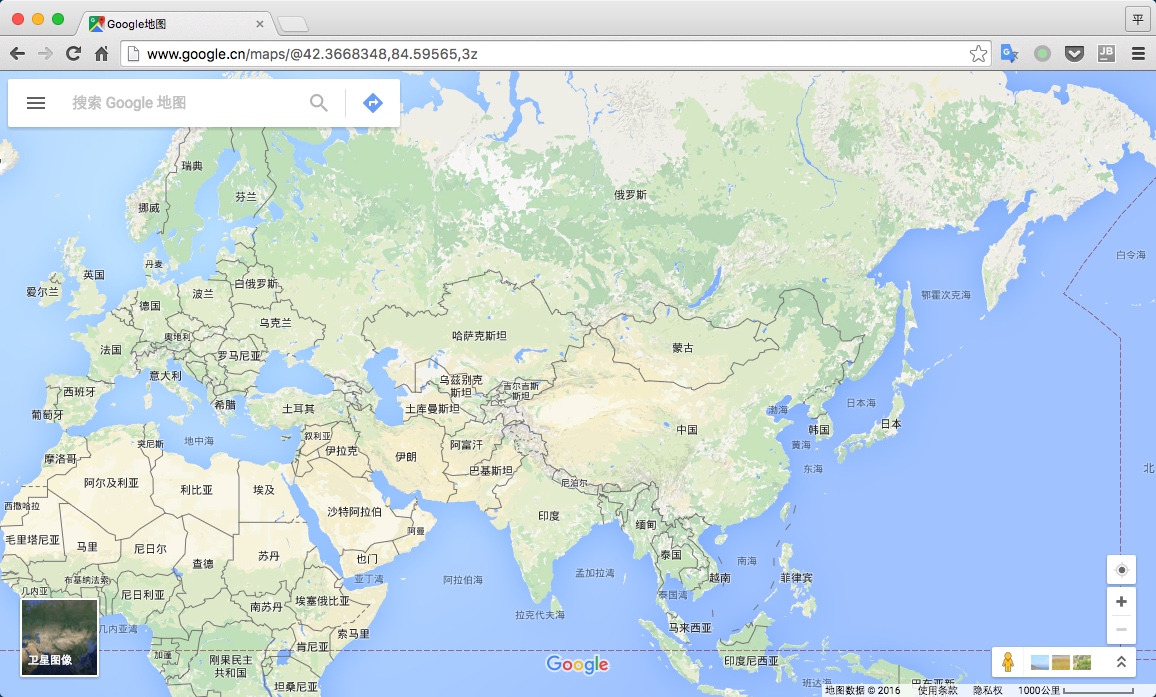
在数据还没有加载过来的时候,我们可以很容易看到地图中划分的网格。